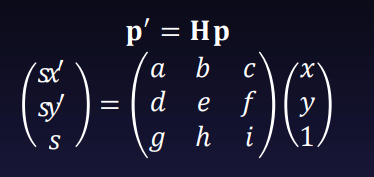homogeneous coordinates
Homogeneous 좌표는 쉽게 말하면 (x, y)를 (x, y, 1)로 표현하는 것이다. 임의의 0이 아닌 상수 w에 대해 (x, y)를 (wx, wy, w)로 표현하는 것
homogeneous 좌표계에서 스케일(scale)은 무시되며 (x, y)에 대한 homogeneous 좌표 표현은 무한히 많이 존재하게 된다.
마찬가지로, 3차원의 경우에는 (X, Y, Z)를 (X, Y, Z, 1) 나 (wX, wY, wZ, w)로 표현한다.
Homogeneous 좌표가 활용되는 곳은 주로 컴퓨터 그래픽스(graphics) 쪽이나 3D 비전 쪽이다. 그 이유는 homogeneous 좌표계를 사용하면 affine 변환이나 perspective(projective) 변환을 하나의 단일(single) 행렬로 표현할 수 있기 때문이다.
우리가 흔히 알고 있는 기하학은 유클리디언 기하학(Euclidean geometry)이며 유클리디언 기하학에서는 데카르트 좌표계(Cartesian coordinate system)를 사용한다. 우리가 익히 알고 있는 직교 좌표계가 바로 이것이다.
하지만 projective geometry에서 사용하는 좌표계는 homogeneous 좌표이며 homogeneous 좌표를 다른 말로 projective 좌표라고도 부른다.
projective geometery 사영 기하학
일단 Projective라는 단어는 투영 또는 사영을 뜻한다. Projective라는 단어는 (3D→2D 한정으로) 우리가 3D 세상의 정보를 2D 이미지에 투영하여 본다는 의미로,
시야라는 뜻을 가진 Perspective라는 단어와 함께 쓰일 수 있다.
사영 기하학은 말 그대로 프로젝션(projection)을 다루는 기하학이며 homogeneous(projective)좌표계를 사용한다. Projective geometry는 어떤 물체를 바라보는 시야를 수학적/기하학적으로 표현하는 방법이다.
2차원 사영 기하학에서 두 homogeneous 좌표 (x, y, 1), (2x, 2y, 2)는 서로 같다. 왜냐하면 두 점 모두 동일한 한 점 (x, y)로 투영되기 때문.
사영 기하학에서는 길이(length), 각도(angle), 평행성(parallelism)이 보존되지 않는다. 이는 3D 공간의 물체를 2D 영상에 투영시켜 보면 쉽게 확인할 수 있다. 다음의 사진을 보면,
사영 기하학에서 보존되는 것은 type이다. 즉, 직선은 직선으로 투영되고 곡선은 곡선으로 투영된다. 물론 직선 중에는 한 점으로 투영되는 경우도 있을 수 있다.
Homograpy (Projective Transformation)&(Perspective Transformation)
Perspective transformation은 3D→2D Projective transformation 방법 중 하나인데, 원근법을 가지고 3D 세상 → 2D 이미지 투영을 할 때 사용할 수 있다.
카메라 모델링에서는 Perspective transformation을 주로 고려하기 때문에, Projective~ 로 시작하면 일단 간단하게 ‘어떤 물체를 바라보는 시야를 표현하는 방법’ 이라고 생각하면 굉장히 쉽게 생각할 수 있다.
Projective transformation은 가장 상위 단계로써 Affine transformation에서 이제 직선들의 평행성까지 사라진 transformation이다. Projective transformation 후에도 유지가 되는것은 오직 직선간의 교차점 (incidence)와 비조화비 (cross-ratio) 밖에 없다. 사람의 시야가 실제로 평행한 철로를 바라볼 때 철로가 사다리꼴 모양이 되는 이유는, 원근법이 적용되면서 Projective transformation이 적용되기 때문이다. 이렇게 원근법 + Projective transformation이 동시에 적용될 때 우리는 이런 변화를 perspective transformation이라고 부른다.
2D Projective transformation에는 또 다른 이름이 하나 있는데, 2D→2D projective transformation (또는 perspective transform)에 대해서 Homography라는 이름으로 부른다.
Homography는 homogeneous 좌표계에서 정의되며 그 일반식은 다음과 같다.
Homography는 자유도가 8이며 따라서 homography를 결정하기 위해서는 최소 4개의 매칭쌍을 필요로 한다. Homography의 자유도가 9가 아니라 8인 이유는 (x,y,1), (sx’,sy’,s)이 homogeneous 좌표이므로 homography의 scale을 결정할 수 없기 때문이다 (∵ homography 변환 p’=Hp에서 p, p’은 homogeneous 좌표이기 때문에 p’= λHp도 성립하게 된다. 즉, H가 homography 행렬이라면 임의의 0이 아닌 λ에 대해 λH도 또한 동일한 homography 행렬이다).
2d 변환이라고 앞에서 살펴본 변환들은 모두 Affine Transformation 이다. 따라서 기본적으로 affine 변환 행렬을 통하여 변환할 수 있었다.
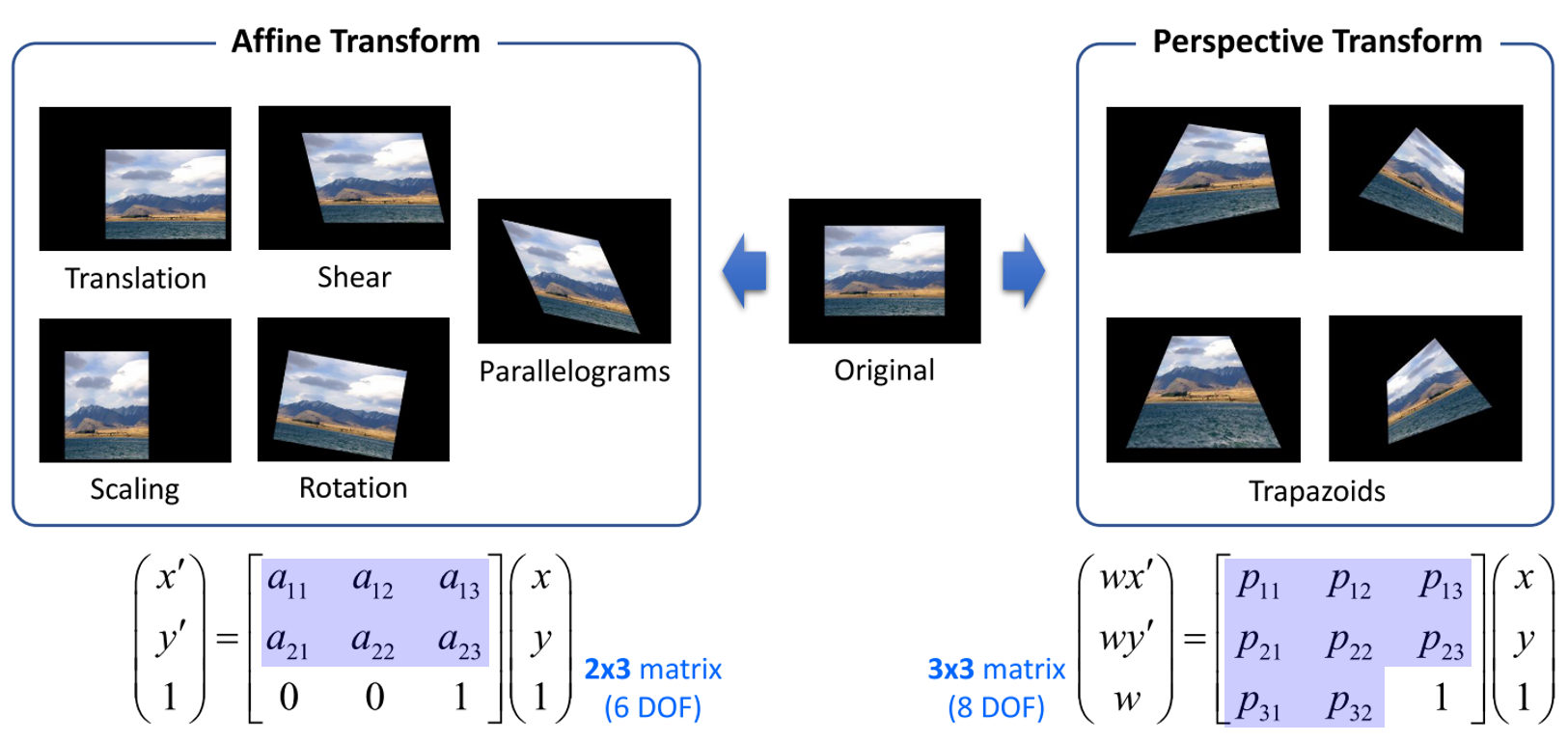
Affine Transformation의 공통점은 변환 결과가 모두 평행사변형(Parallelograms)이라는 점 이다. 즉, 앞에서 다룬 이동 변환, 전단 변환, 크기 변환, 대칭 변환, 회전 변환의 결과는 모두 평행 사변형 꼴의 변환이다. 호모지니어스 형태의 Affine Transformation을 perspective transformation 과 비교해보자.
먼저 Affine Transformation은 6개의 파라미터를 가진다. 여기서 파라미터를 DOF(Degree Of Freedom)이라고 하며 DOF를 통하여 자유롭게 변형이 이미지의 기하학적 변환이 가능하기 때문에 이와 같은 이름으로 부른다.
Affine Transformation에서는 위 변환 행렬에서 2 X 3 행렬 크기의 파란색 음영의 6개 DOF가 정해지면 그 값에 맞춰서 이동, 전단, 크기, 대칭, 회전 등의 변환을 하게 된다.
반면 Perspective Transformation에서는 3 X 3 행렬에서 파란색 음영의 8개 DOF가 정해지면 그 값에 맞춰서 변환을 하게 된다.
변환된 이미지의 모양을 보면 평행사변형(Parallelograms) 형태의 Affine Transformation 보다 Perspective Transform이 더 자유로운 모양을 띄게 된다. 그 이유는 DOF가 2개 더 많기 때문에 자유로움이 더 높이 때문.
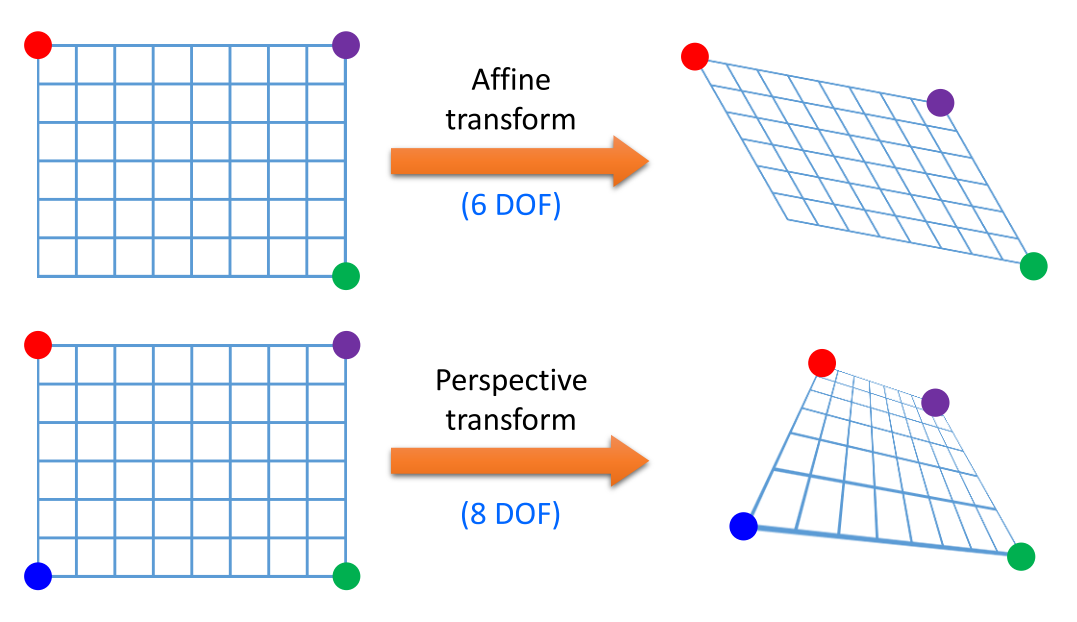
Affine Transformation에서 6개의 파라미터를 알기 위해서는 6개의 연립 방정식이 필요합니다. 1개의 (x, y)에 대한 homogeneous 행렬에서 DOF에 관한 2개의 식을 구할 수 있기 때문에 3개 점의 6개 식을 이용하면 6개의 DOF를 구할 수 있다. 이는 위 그림과 같이 Affine Transformation이 평행사변형 형태를 유지하는 변환이기 때문에 3개의 점을 지정하면 자동적으로 하나의 점이 고정이 되어 3개의 점을 통해 변환 행렬을 구할 수 있는 것과 의미가 같다. 따라서 3개의 점의 변환 전 좌표와 변환 후 좌표를 알아야 Affine 변환 행렬을 구할 수 있다.
이와 동일한 관점에서 Perspective Transformation은 8개의 DOF를 구하기 위하여 4개의 점을 사용하여 구할 수 있다. 이는 위 그림과 같이 Perspective Transformation에서는 4개의 꼭지점이 자유롭게 변환된 상태로 이미지를 변환할 수 있어야 하기 때문에 4개의 점의 변환 전 좌표와 변환 후 좌표를 알아야 Perspective 변환 행렬을 구할 수 있다.
*본 포스팅은 주로 다크 프로그래머님의 블로그를 기반으로 작성한 글입니다.
참고 https://gaussian37.github.io/vision-concept-image_transformation
https://gaussian37.github.io/vision-concept-homogeneous_coordinate
https://cvlearnblog.notion.site/3D-2D-2-Introduction-to-Projective-Geometry-03144b584c1d47d686c7ab5dadd2bfab